전체 확률의 법칙
== 개요 ==* 본 문서는 현재 위키 문법 버그로 인해 수식이 제대로 표기되지 않았습니다.
전체 확률의 법칙(law of total probability) 또는 전확률 정리는 조건부 확률과 관계된 법칙이다. 조건부 확률로부터 조건이 붙지 않은 확률을 계산할 때 쓸 수 있다. 또한 베이즈 정리 공식의 일부에 전확률 정리 공식이 들어간다.
사상(집합) A는 사상 B의 부분 사상이고, 사상 B가 사상 B1, B2, ..., Bk로 나눌 수 있을 때 전확률 공식이 성립한다.
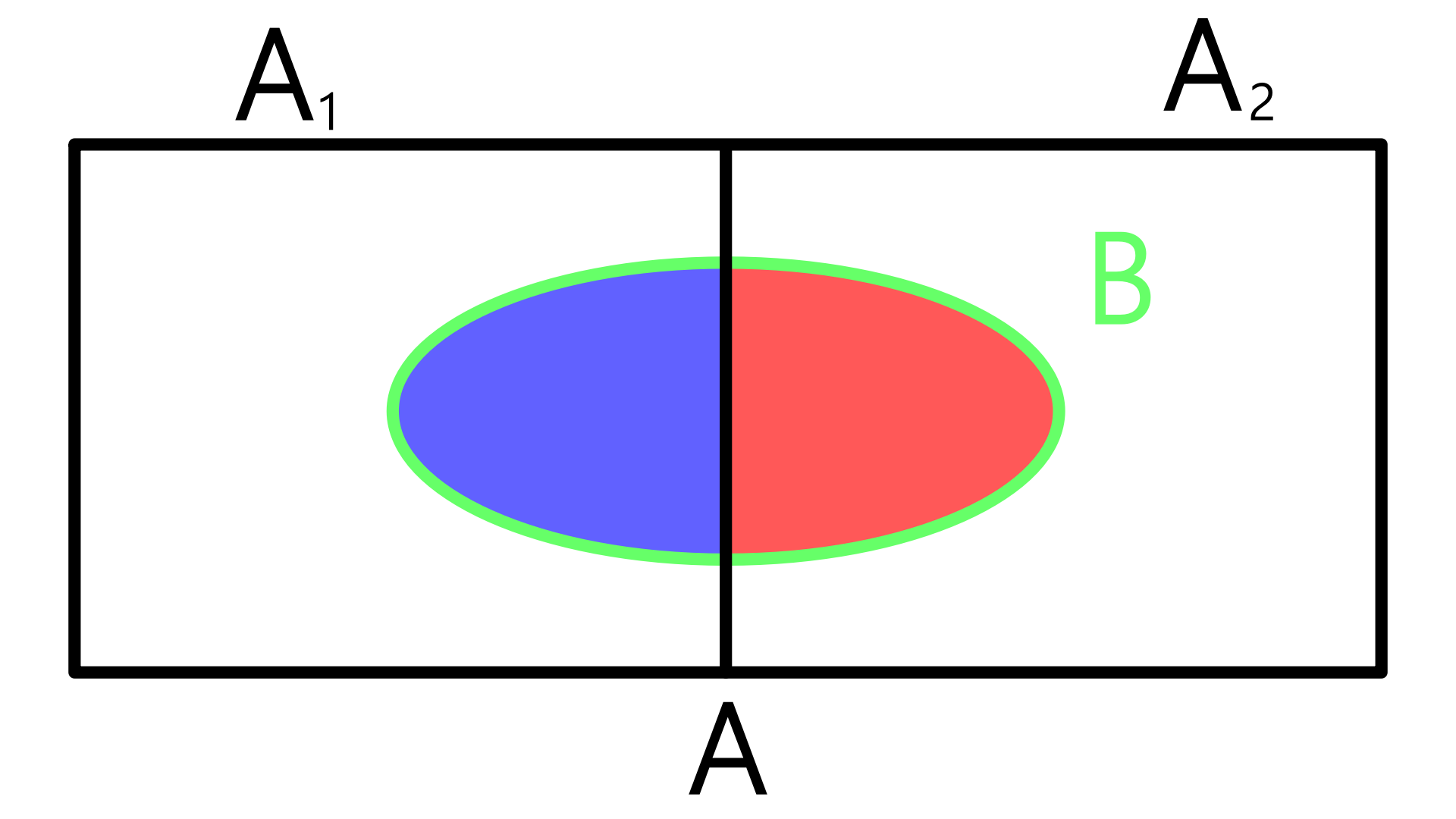 ||||== 정리 유도 ==조건 1. B는 상호 배타적임. ()조건 2. B의 합집합은 전체 표본공간임. ()||||
||||== 정리 유도 ==조건 1. B는 상호 배타적임. ()조건 2. B의 합집합은 전체 표본공간임. ()||||
== 관련 문서 == * 조건부 확률 * 곱셈 공식 * 베이즈 정리
전체 확률의 법칙(law of total probability) 또는 전확률 정리는 조건부 확률과 관계된 법칙이다. 조건부 확률로부터 조건이 붙지 않은 확률을 계산할 때 쓸 수 있다. 또한 베이즈 정리 공식의 일부에 전확률 정리 공식이 들어간다.
사상(집합) A는 사상 B의 부분 사상이고, 사상 B가 사상 B1, B2, ..., Bk로 나눌 수 있을 때 전확률 공식이 성립한다.
 ||||== 정리 유도 ==조건 1. B는 상호 배타적임. ()조건 2. B의 합집합은 전체 표본공간임. ()||||
||||== 정리 유도 ==조건 1. B는 상호 배타적임. ()조건 2. B의 합집합은 전체 표본공간임. ()||||== 관련 문서 == * 조건부 확률 * 곱셈 공식 * 베이즈 정리